红与黑的秘密——红黑树
上次小编分享了AVL树
那么这个AVL树呢,由于涉及到比较多的旋转,所以呢,一旦进行了对的树的修改操作
就显得性能较为低下,所以AVL树呢,一般适合静态数据的查找。
那么有没有一种既可以较为高效的查找,且也对树的结构进行操作,但并没有造成性能较为低下的数据结构呢?
那么此时主角登场——
红黑树
那么红黑树是什么呢?
这个红黑树也是一种二叉搜索树,但是呢,在每个节点上增添一个可以表示节点颜色的存储位
,那么可以表示Red、Black,并满足一定的条件来保证树的平衡。
那么可以通过对任何一条根从叶子的路径上结点着色方式的限制,红黑树确保没有一条路径比其他路径长出两倍,因而这是接近平衡的。
这里要值得说明的是,红黑树呢是相对平衡的,
相对平衡:其左右子树高度差与其他节点的高度差保持在一定的范围内
绝对平衡:指的是每个节点的左右子树的高度差不超过1
那么给个图片看看吧
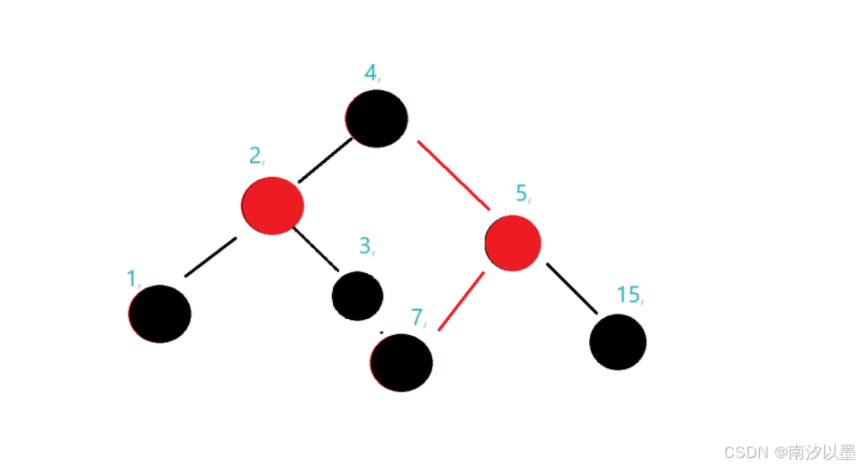
那么此时呢,这个红黑树是具有这样一定的性质的
1.每个节点不是黑色就是红色
2.根节点是黑色的
3.如果一个节点是红色的,则它的两个孩子节点是黑色【没有连续出现的黑色节点】
4.对于每个结点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点
5.每个叶子节点都是黑色的(此处的叶子节点指空节点,是黑色的)
除此之外呢,还有一个推导出来的性质
即最长路径最多是最短路径的两倍
那么这又是什么意思呢?
举个例子:
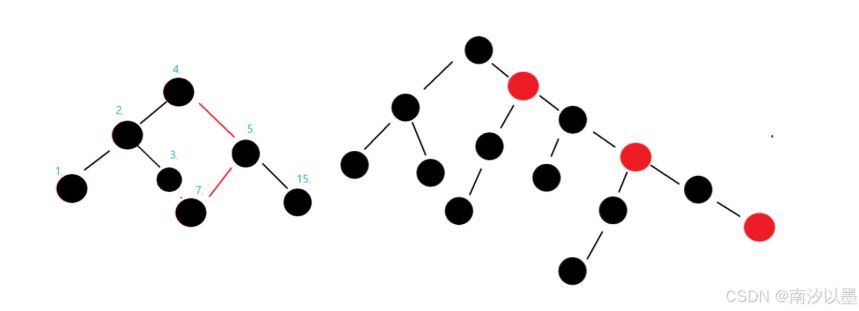
这里是左边这幅图是比较极端情况下的,毕竟也没有说一定不能全是黑色的
那么此时左边这幅图每条路径上是有三个节点的
右边这幅图,最右边的路径达到了6个节点,显然,并没有超出两倍。
那么值得注意的是,一个正常的红黑树,是不会出现全部都是黑色节点,或者一条路径上全部是黑色节点
到这里呢,提出一个有点意思的问题
加入一个红黑树中的黑色节点为X个,那么这个树的总节点N,范围在哪里?
其实刚刚那个上述举的例子中可以看的出来,
全为黑:x个
一黑一红交替出现:2X
范围表示为【x,2x】
那么此时又可以得出一个这样的结论
最短路径长度:logN
最长路径长度:log2N=2*logN
那么可以看到其实,两者相差不了多少的。
那么性质什么的讲完了,接下来讲讲如何实现吧。
实现这里,小编呢讲讲的是插入。
插入
那么上述讲到,这个红黑树也是一颗平衡二叉树。
那么这里,既然是红黑树,有了颜色的标记,所以,我们可以定义一个枚举类,来表示红色、黑色
代码如下:
public enum Color {
Red,Black;
}
所以我们定义的节点中,可以包含颜色了。
那么这个红黑树定义的节点代码如下:
public class RBTree {
static class Node{
public int val;
public Node left;
public Node right;
public Node parent;
//此时用到一个枚举类的颜色,默认红色
//默认为红色,插入节点只需调节颜色,默认为黑色,就要插入无关的节点
public Color color;
public Node(int val){
this.val=val;
this.color=Color.Red;
}
}
那么这里需要解释下为什么插入节点默认的颜色为红色。
因为,我们要是插入新的节点颜色为黑色,比如以下这个例子: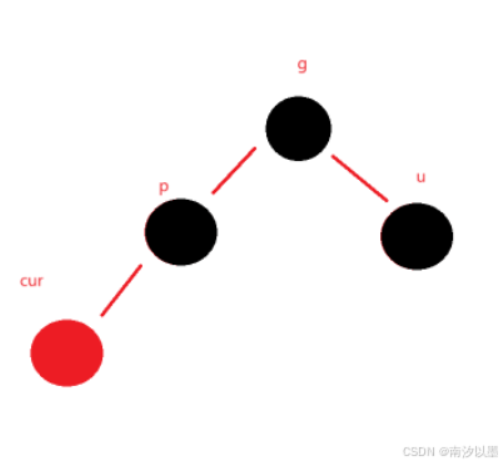
如若在p中插入节点,为了保证红黑树中这个性质:每条路径上的黑色节点必须是相同数目
此时,也要往根节点的右树插入两个黑色节点,以保证这个数目是相同的。
那么这个平衡二叉树的插入前些部分操作和之前实现的AVL树是类似的
代码如下:
public Node root;
public boolean insert(int val){
//插入的方式和AVL树中部分类似,即调整平衡因子前的代码,可以迁移过来
Node newnode=new Node(val);
if(root==null){
root=newnode;
root.color=Color.Black;
return true;
}
Node parent=null;
Node cur=root;
while (cur!=null){
if(cur.val<val){
parent=cur;
cur=cur.right;
}else if(cur.val>val){
parent=cur;
cur=cur.left;
}else {
return false;
}
}
if(parent.val<val){
parent.right=newnode;
}else {
parent.left=newnode;
}
newnode.parent=parent;
cur=newnode;
//此时要进行颜色调节
值得注意的是,我们的根节点是黑色的,所以当插入第一个节点的时候,要手动设置为黑色
那么我们插入节点的时候就会遇到两个节点是红色的,所以此时违反了红黑树的性质,那么就要进行颜色的调节
进行调节之前,先约定一些节点定义
cur为当前节点、parent为cur的父亲节点、gandfacter为parent的父亲节点、uncle为叔叔节点
后面图片中标记时,逐一简写,c、p、g、u
当插入的节点cur的父亲节点在左边为一种情况,在右边又是一种情况。
cur的父亲节点在左边
情况一:cur为红色、p为红色,u存在且为红色
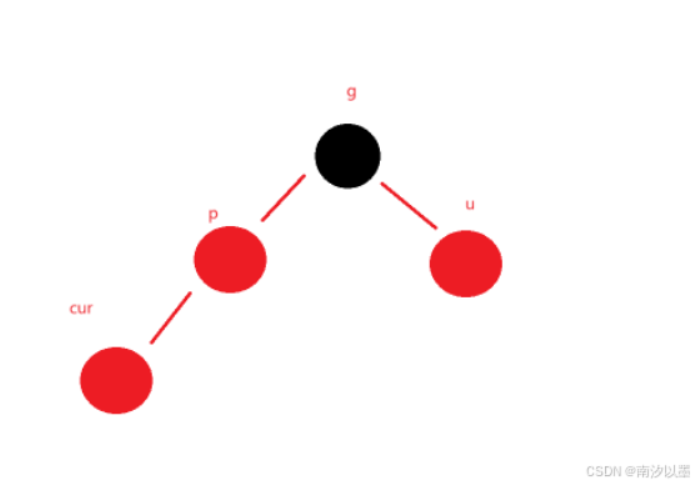
思路:
把p颜色标记为黑色,u的节点标记为黑色
完了?还没有!
g也有父亲节点,且g的父亲节点也可能为红色和黑色
比如下面的情况
情况一分支一:
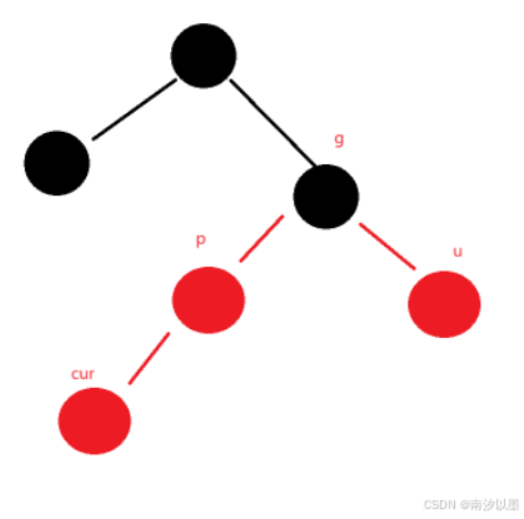
那么此时我们单纯的将其p、u颜色设置为黑色是不行的,这样会导致每条路径上的黑色节点数目不一致,所以还是需要将g的节点设置为红色
修改后:
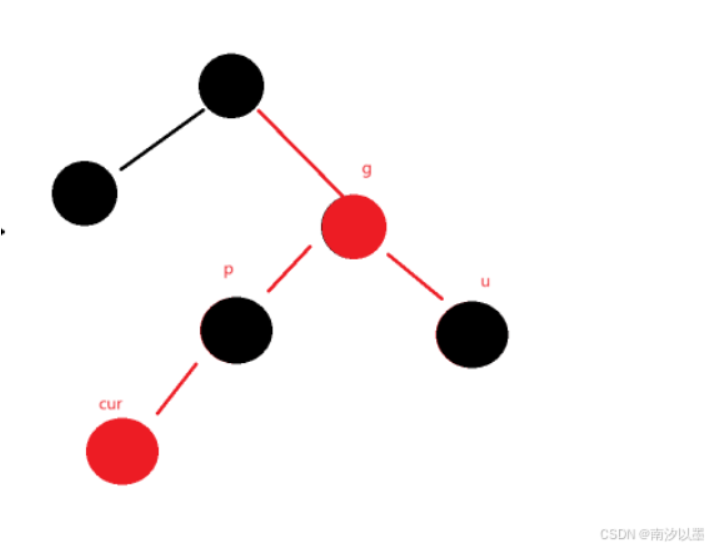
情况一分支二:
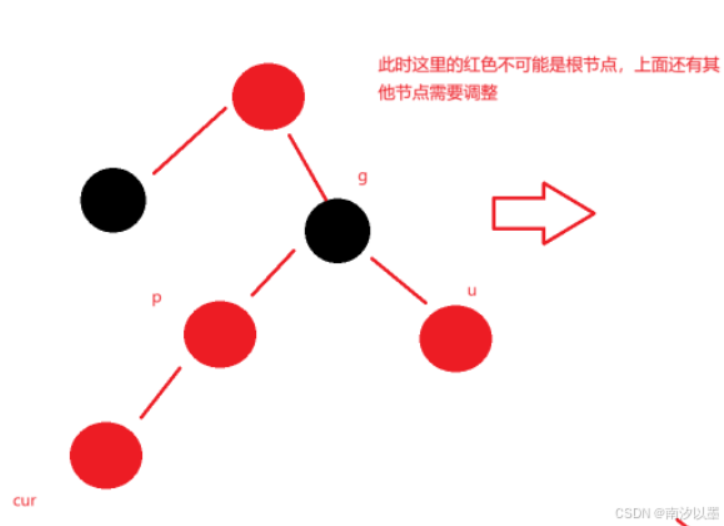
那么此时将p、u的颜色设置为黑色,如何将这个g设置为红色后,
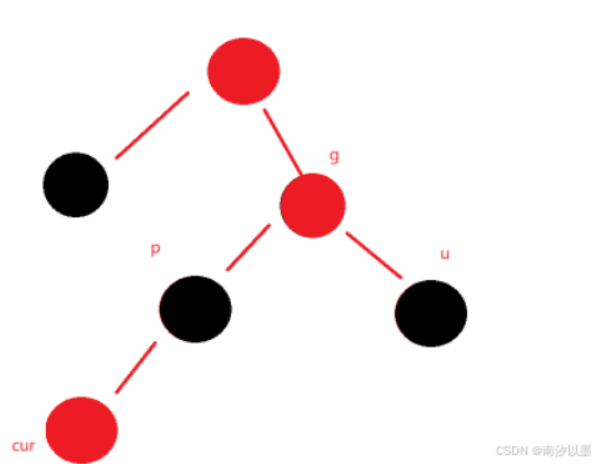
那么此时又发现违反了性质了,那么继续向上调整
cur=g,p=cur.parent
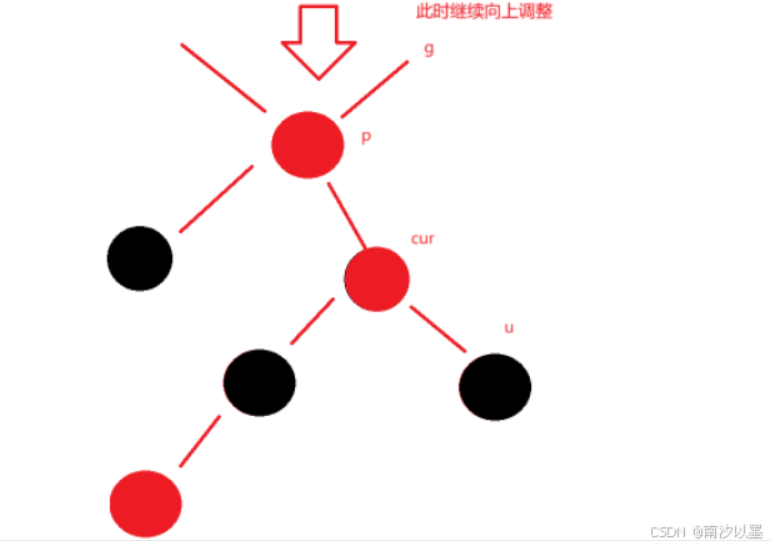
此时直到parent节点为null,调整就结束了
那么这里是有点小问题还没有解答,万一它就只有一个根节点,此时就是为黑色的呢,那么这时候呢,所有情况调整完后,再次把它设置为黑色,所以在这之前,情况一,统一设置为红色,对于这个根节点来说。
情况一代码:
while (parent!=null&&parent.color==Color.Red){
//连接两个红色节点的时候,就要调整,
//即检查父亲节点是否为红色节点即可
//首先定义祖父节点这个点先
Node grandFacter=parent.parent;
if(parent==grandFacter.left){
//情况一:cur为红,p为红,g为黑,u存在且为红
Node uncle=grandFacter.right;
if(uncle!=null && uncle.color==Color.Red){
parent.color=Color.Black;
uncle.color=Color.Black;
grandFacter.color=Color.Red;
//此处将grandFacter设置为红,是怕存在grandFacter的父亲节点,
//如若没有,后续统一设置为黑色
//为了防止当前的grandFacter存在父亲节点,即向上调整
cur=grandFacter;
parent=cur.parent;
那么情况二又是什么呢?
上述说到uncle是红色,且存在的,那么这里呢,就是说u是不存在或者是黑色的
情况二:cur为红色,parent为红色,g为黑色,u不存在/为黑色
举个例子:
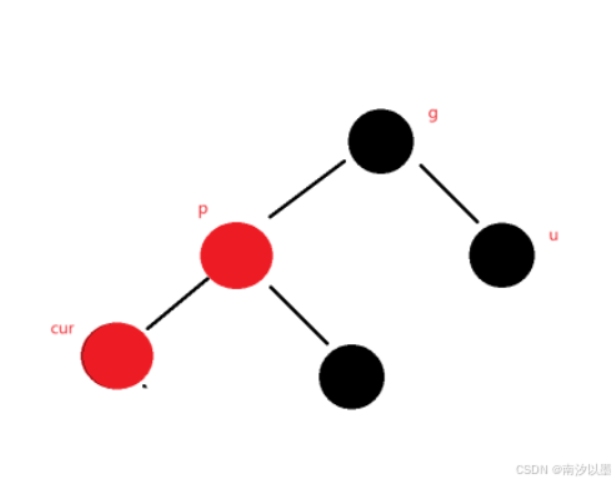
此时,我们发现,这里很奇怪,正常来说,这里黑色节点不符合其性质,而且又有两个红色节点在这,那么,怎么得来的情况呢?
这个情况就是调整过程中出现的
出现此过程如下:
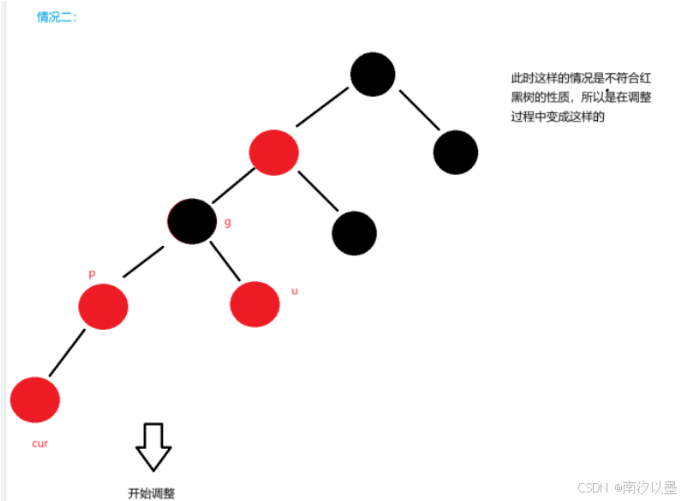
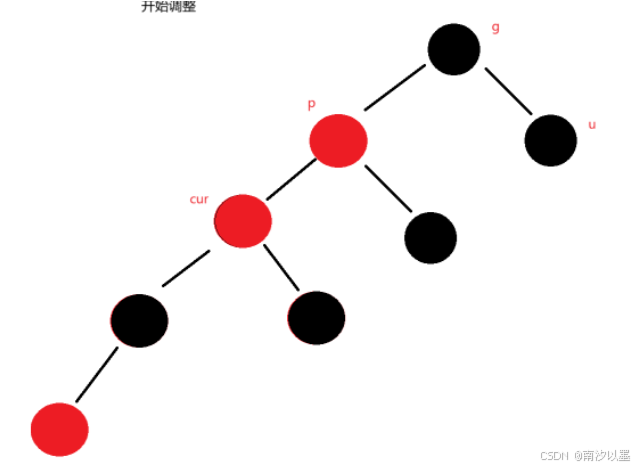
这里的调整是按照情况一那样进行调整的。
情况是符合了,那么解决方案是?
思路:左边高,进行右单旋,然后修改parent和grandFacter的颜色
为什么要修改颜色,不修改颜色的话,此时每条路的黑色节点数目不一致了,
然后这个右单旋,AVL树中分享过了,小编呢,在这不做过多赘述
那么,情况二的代码先不放出来,接着介绍情况三,到时候会有个惊奇的发现
情况三:cur为红,parent为红,gandfacter为黑,u为黑/不存在
这里怎么感觉和情况二一样呢?
上图先:
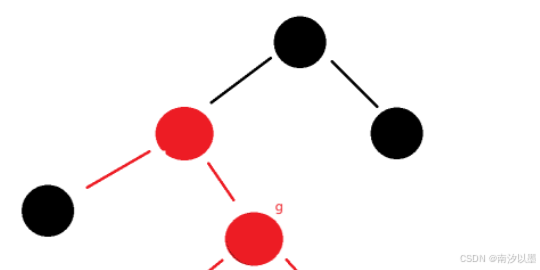
那么此时可以发现,不一样的地方,新插入的cur节点在这个红色节点的右边了,情况二在左边的,所以这里是不一样的地方。
那么显然,正常来说,不能是无缘无故到这个情况的,那么这个也是调整过程中出现的
调整过程中:
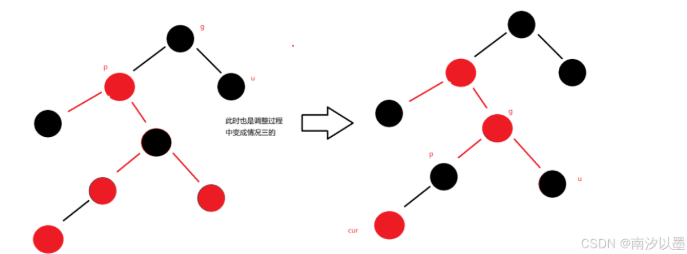
思路:
右树变高了,左单旋
然后不修改颜色了?
当然不是,且看旋转后的结果
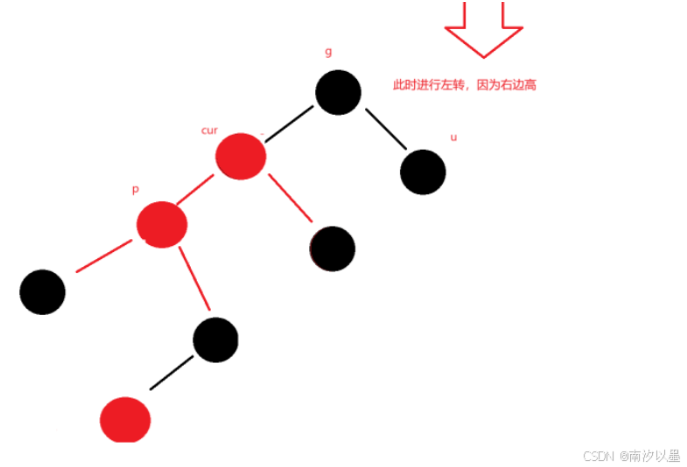
你会发现,似曾相识
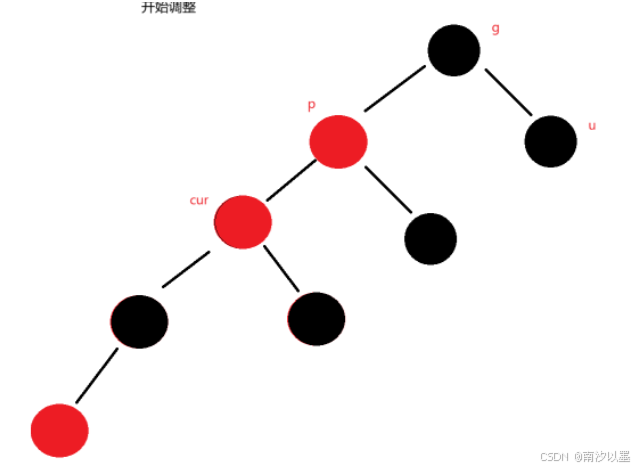
这不就是和情况二差不多嘛,只不过是,cur和parent的位置不同而已,
所以这时候,我们执行cur和parent调换操作,然后再次执行情况二的操作就行
所以在代码方面呢,我们先把情况三处理了,将情况三处理成情况二后,再次执行情况二的操作即可
代码:
}else {
//即uncle不存在或者为黑色,和情况二情况三的有点类似
//情况三: cur为红,p为红,g为黑,u不存在/u为黑,此时cur在parent的右边
//先处理情况三,使其变成情况二,
if(parent.right==cur){
rotateLeft(parent);
//交换节点位置,使其变成情况二
Node temp=parent;
parent=cur;
cur=temp;
}
//此时处理情况二 cur为红,p为红, g为黑,u不存在/u为黑,
//右转,因为左边高
rotateRight(grandFacter);
grandFacter.color=Color.Red;
parent.color=Color.Black;
}
}
到这里出现情况的讲解完成了
此时呢,我们还得处理cur的父亲节点在右边的情况
cur的父亲节点在右边
那么这种情况中,其里面的遇到一些情况一、二、三是和cur的父亲节点在左边(即上述刚刚说的)是差不多的,只是要修改几个值而已,所以下面呢就给出图片,思路不做解释了,毕竟思路和刚刚上面是差不多的
情况一:
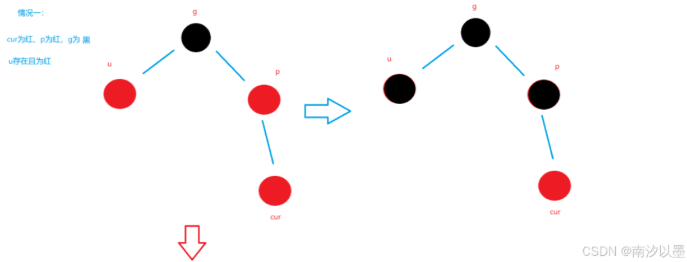
情况一分支一:
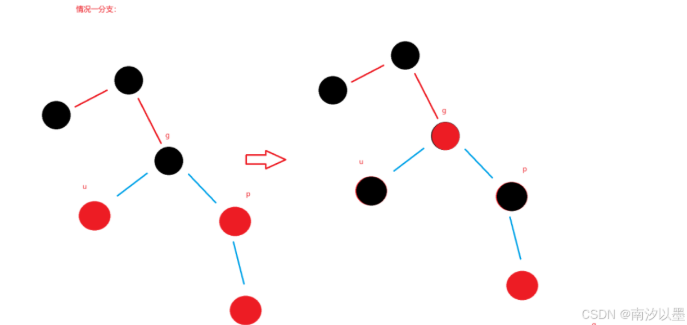
情况一分支二:
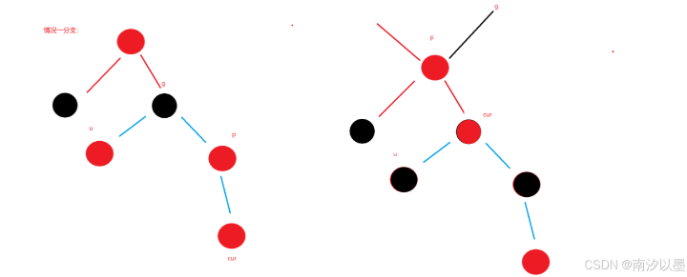
情况二:
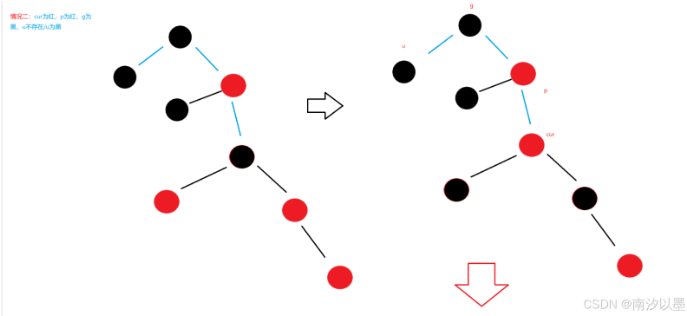
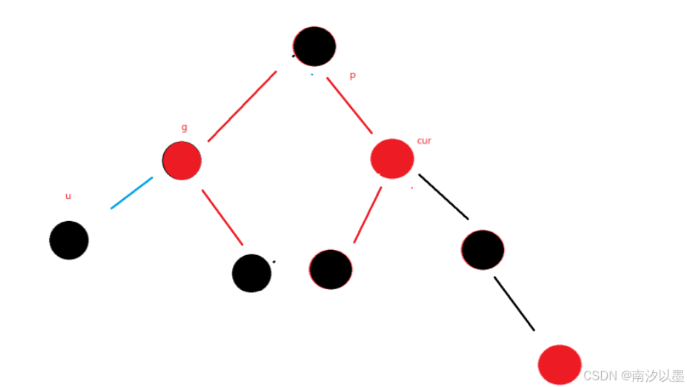
情况三:
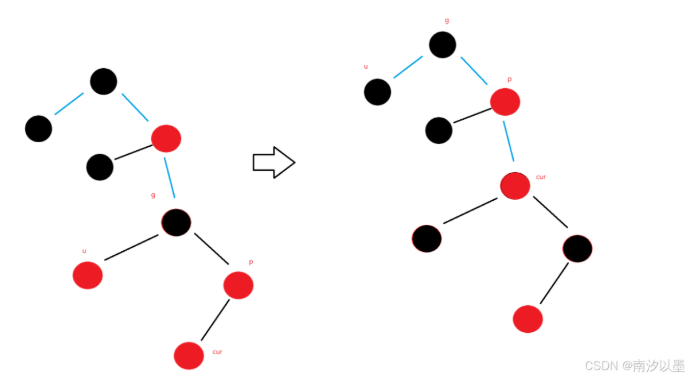
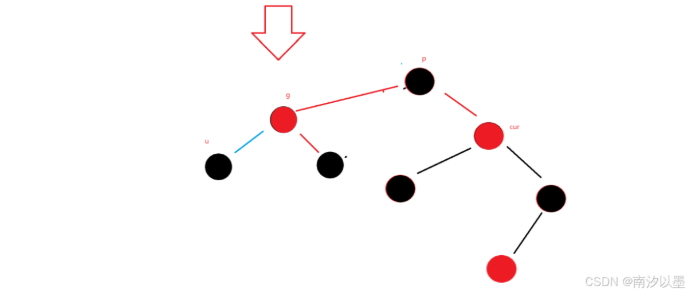
此时我们发现,cur的parent在右边的情况中,仅仅是以下这些有改变
uncle改变,为grandFacter.left
后面的对应旋转,从情况三的左单旋,变成右单旋
情况二中的右单旋,变成左单旋。
那么直到这里,红黑树的插入操作讲解完毕了
那么这个删除操作,就不做讲解了,这里分享其他博主写的两篇博客,大家有兴趣的可以看看
删除
一步一图一代码,一定要让你真正彻底明白红黑树_红黑书排序-CSDN博客
那么问题又来了,如何判断我们输入的红黑树,它就是一定符合其性质的呢?
判断树是否符合红黑树的性质
刚刚我们上述讲到的性质如下:

所以,在这里呢,我们仅需判断我们输入的数据,是否符合性质2、3、4即可,
因为性质1、性质5是在判断符合2、3、4性质的时候,包含了此判断。
判断是否符合性质2
思路:如若根节点不是黑色,那么打印对应的信息,然后返回false。当然这个false我这里放到最后返回,因为其他两个性质没有判断
判断是否符合性质3
思路:递归,类似于之前的二叉树遍历,遇到当前节点的颜色为红色,然后呢,判断其父亲节点是否为红色,若是,即不符合性质3
判断是否符合性质四:
思路:我们这里呢,先寻找到其中一条路径中黑色节点的个数——blackNum,然后将其保存下来
接着,去递归红黑树的每一条路径,这里的递归还是类似于二叉树的遍历操作,所以
一旦发现blackNum和递归每一条路径时,所计算的黑色节点不一致,就返回false
那么代码如下:
public boolean isRBTree(){
if(root==null){
//空树也是一颗红黑树
return true;
}
if(root.color!=Color.Black){
System.out.println("违反性质:根节点必须为黑色");
}
int blackNum=0;
Node cur=root;
while (cur!=null){
if(cur.color==Color.Black){
blackNum++;
}
cur=cur.left;
}
return checkColor(root)&&checkNum(root,0,blackNum);
}
/**
*
* @param root
* @param pathNum 这里是当前路径的节点
* @param blackNum 这个是isRBTree()方法中给定的,计算出一条路径上有多少个节点
*/
public boolean checkNum(Node root,int pathNum,int blackNum){
if(root==null){
return true;
}
if(root.color==Color.Black){
pathNum++;
}
if(root.left==null&&root.right==null){
if(pathNum!=blackNum){
System.out.println("违法性质:每条路径上的黑色节点不一致");
return false;
}
}
return checkNum(root.left,pathNum,blackNum) && checkNum(root.right,pathNum,blackNum);
}
public boolean checkColor(Node root){
if(root==null){
return true;
}
if(root.color==Color.Red){
Node parent=root.parent;
if(parent.color ==Color.Red){
System.out.println("违反性质:不能有两个连续的红色节点");
return false;
}
}
return checkColor(root.left) && checkColor(root.right);
}
源码:
Color类:
public enum Color {
Red,Black;
}
RBTree类:
public class RBTree {
static class Node{
public int val;
public Node left;
public Node right;
public Node parent;
//此时用到一个枚举类的颜色,默认红色
//默认为红色,插入节点只需调节颜色,默认为黑色,就要插入无关的节点
public Color color;
public Node(int val){
this.val=val;
this.color=Color.Red;
}
}
public Node root;
public boolean insert(int val){
//插入的方式和AVL树中部分类似,即调整平衡因子前的代码,可以迁移过来
Node newnode=new Node(val);
if(root==null){
root=newnode;
root.color=Color.Black;
return true;
}
Node parent=null;
Node cur=root;
while (cur!=null){
if(cur.val<val){
parent=cur;
cur=cur.right;
}else if(cur.val>val){
parent=cur;
cur=cur.left;
}else {
return false;
}
}
if(parent.val<val){
parent.right=newnode;
}else {
parent.left=newnode;
}
newnode.parent=parent;
cur=newnode;
//此时要进行颜色调节
while (parent!=null&&parent.color==Color.Red){
//连接两个红色节点的时候,就要调整,即检查父亲节点是否为红色节点即可
//首先定义祖父节点这个点先
Node grandFacter=parent.parent;
if(parent==grandFacter.left){
//情况一:cur为红,p为红,g为黑,u存在且为红
Node uncle=grandFacter.right;
if(uncle!=null && uncle.color==Color.Red){
parent.color=Color.Black;
uncle.color=Color.Black;
grandFacter.color=Color.Red;
//此处将grandFacter设置为红,是怕存在grandFacter的父亲节点,如若没有,后续统一设置为黑色
//为了防止当前的grandFacter存在父亲节点,即向上调整
cur=grandFacter;
parent=cur.parent;
}else {
//即uncle不存在或者为黑色,和情况二情况三的有点类似
//情况三: cur为红,p为红,g为黑,u不存在/u为黑,此时cur在parent的右边
//先处理情况三,使其变成情况二,
if(parent.right==cur){
rotateLeft(parent);
//交换节点位置,使其变成情况二
Node temp=parent;
parent=cur;
cur=temp;
}
//此时处理情况二 cur为红,p为红, g为黑,u不存在/u为黑,
//右转,因为左边高
rotateRight(grandFacter);
grandFacter.color=Color.Red;
parent.color=Color.Black;
}
}else {
//这里的情况是uncle在左边了,那么情况呢上面是相反的,其实是差不多的
Node uncle=grandFacter.left;
if(uncle!=null&&uncle.color==Color.Red){
parent.color=Color.Black;
uncle.color=Color.Black;
grandFacter.color=Color.Red;
cur=grandFacter;
parent=cur.parent;
}else {
//情况三
if(parent.left==cur){
rotateRight(parent);
Node temp=parent;
parent=cur;
cur=temp;
}
//情况二:
rotateLeft(grandFacter);
grandFacter.color=Color.Red;
parent.color=Color.Black;
}
}
}
root.color=Color.Black;
return true;
}
public void rotateLeft(Node parent){
//首先定义两个节点
Node subR=parent.right;
Node subRL=subR.left;
parent.right=subRL;
subR.left=parent;
//subRL此时有可能为空,需要判断下
if(subRL!=null){
subRL.parent=parent;
}
//此时有可能parent的parent不为空,所以修改parent.parent指向之前,保存一下
Node pParent=parent.parent;
parent.parent=subR;
//到这里要修改下parent的parent的指向了
if(root==parent){
root=subR;
root.parent=null;
}else {
if(pParent.left==parent){
pParent.left=subR;
}else {
pParent.right=subR;
}
subR.parent=pParent;
}
}
private void rotateRight(Node parent){
//首先定义两个节点
Node subL=parent.left;
Node subLR=subL.right;
parent.left=subLR;
subL.right=parent;
//有可能subL的左边节点为空,那么就要判断一下
if(subLR!=null){
subLR.parent=parent;
}
Node pParent=parent.parent;
//修改parent.parent的节点之前要保存一下parent.parent,有可能当前的parent上面还有一个节点
parent.parent=subL;
//下面修改subL的指向
if(parent==root){
//parent就是头节点
root=subL;
root.parent=null;
}else {
if (pParent.left == parent) {
//如果parent的父亲节点左边等于parent,那么代表着parent左边要连接subL
pParent.left = subL;
} else {
pParent.right = subL;
}
//无论怎么样,subL的父亲节点永远都是pParent
subL.parent=pParent;
}
}
public boolean isRBTree(){
if(root==null){
//空树也是一颗红黑树
return true;
}
if(root.color!=Color.Black){
System.out.println("违反性质:根节点必须为黑色");
}
int blackNum=0;
Node cur=root;
while (cur!=null){
if(cur.color==Color.Black){
blackNum++;
}
cur=cur.left;
}
return checkColor(root)&&checkNum(root,0,blackNum);
}
/**
*
* @param root
* @param pathNum 这里是当前路径的节点
* @param blackNum 这个是isRBTree()方法中给定的,计算出一条路径上有多少个节点
*/
public boolean checkNum(Node root,int pathNum,int blackNum){
if(root==null){
return true;
}
if(root.color==Color.Black){
pathNum++;
}
if(root.left==null&&root.right==null){
if(pathNum!=blackNum){
System.out.println("违法性质:每条路径上的黑色节点不一致");
return false;
}
}
return checkNum(root.left,pathNum,blackNum) && checkNum(root.right,pathNum,blackNum);
}
public boolean checkColor(Node root){
if(root==null){
return true;
}
if(root.color==Color.Red){
Node parent=root.parent;
if(parent.color ==Color.Red){
System.out.println("违反性质:不能有两个连续的红色节点");
return false;
}
}
return checkColor(root.left) && checkColor(root.right);
}
//中序遍历
public void inorder(Node root){
if(root==null){
return;
}
inorder(root.left);
System.out.print(root.val+" ");
inorder(root.right);
}
}
那么到这里,红黑树的分享到此完毕。
