堆:让数据乖乖站好队
今天学习了一种数据结构,一种有趣的数据结构——堆。
所以让我来浅谈一下吧。
首先在认识堆之前,我们讲另一个东西。
在我之前的文章介绍了队列(一种先进先出的数据结构),但是吧,我们有些情况下,我们弹出数据的时候,可能会带上优先级,一般出队列的时候,可能需要优先级高的元素先出队列。
在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数 据结构就是优先级队列(Priority Queue)
而在我们的java中,我们的优先级队列底层是使用了堆这种数据结构。
OK,讲到这里大概就行了。
接下来介绍真正的嘉宾——堆。
堆:
概念:如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一 个一维数组中,并满足:Ki = K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大 堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
按照概念呢,我们引出一些性质:
1.堆中某个节点的值总是不大于或不小于其父节点的值。
2.堆总是一颗完全二叉树。
ok,我们的概念和性质讲完,我们来讲讲这个堆的创建和实现一些相关的功能吧(java语言编写)
首先,我们得首先要有个堆,才能继续实现相关功能。
堆呢又分大根堆和小根堆。
这里我们实现的是大根堆,大根堆实现的话,小根堆也是易实现的。
那我们得怎样创建个大根堆呢?
既然我们先前说了,大根堆的元素是以数组形式的存储的。
那么我们先做好一些基本框架先:
基本结构:
public class MyHeap {
public int []arr;
public int UsedSize;
public MyHeap(){
this.arr=new int [10];
}
}
既然我们数组有了,我们先往这个数组里放入一些数据。
我们可以用一个方法来实现。
public void init(int [] elem){
for (int i = 0; i < elem.length; i++) {
arr[i]=elem[i];
UsedSize++;
}
}
假设我们放的数据是这样的:
27,15,19,18,28,34,65,49,25,37
注意我们放的数据是二叉树层序遍历的结果。
那我们接下来就要将其变成一个大根堆:
首先将这个数据以二叉树的形式表现出来: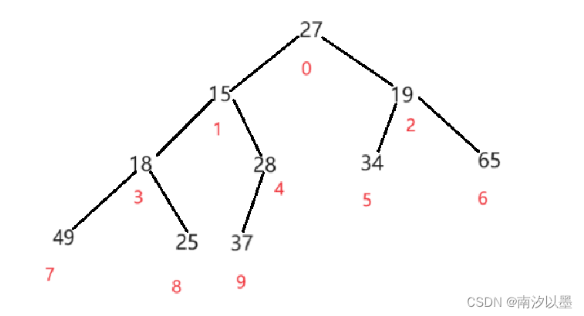
红色的是数组下标。
怎么调整为大根堆呢?
我们以28——37这一颗树来说。
思路:左右孩子最大值,然后根根节点比较,大于,就交换。
28称为parent
37称为child。
当我们28的根节点走完后,我们--,退到了18,以此类推。
那我将这个交换的过程叫做向下调整
至此,我们可以写出一些这样的代码
creatHeap:
public void createHeap(){
for(int parent=(UsedSize-1-1)/2;parent>=0;parent--){
shiftDown(parent,UsedSize);
}
}
至于我们的parent就好确定:(孩子节点-1)/2
为什么我们向下调整的结束条件是UsedSize呢?
我们看回刚刚的那张图片想下。
在28——37那颗树来说,我们肉眼看到就是比较下然后交换就算停止了,但是程序怎么知道呢?
我们就要告诉它,
让这个parent等于child,至于我们的child,知道了parent,child很容易就知道了。
child=2*parent+1。
这样子的话,当我们的parent走到child时,child再走,所以就会发生越界,因为我们的数组长度是10。
所以我们的停止条件就是不能超过这个UsedSize
接下来我们就得实现下shiftDown这个方法了。
先上代码:
shifDown:
public void shiftDown(int parent,int end){
int child=2*parent+1;
while (child<end){
if(child+1<end && arr[child]<arr[child+1]){
child++;
}
if(arr[child]>arr[parent]){
swap(child,parent);
parent=child;
child=2*parent+1;
}else{
break;
}
}
}
private void swap(int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
代码一上来呢,我们就得确定了child的值。
第一个if语句呢
我们要搞定左孩子还是右孩子大。
注意:同时我们也要判断child+1是否合法,如果没有右孩子的话,所以肯定不进去第一个if语句。
第二个if语句
判断我们孩子是否大于父亲节点,如果大于
那么我们就进行交换。parent和child同时也要走。
这样子我们以提供好数据的方式创建一个堆。
那有没有可以不用提供数据来创建一个堆呢?
当然有,那我们介绍另一个方法。
offer:
以这幅图为例:
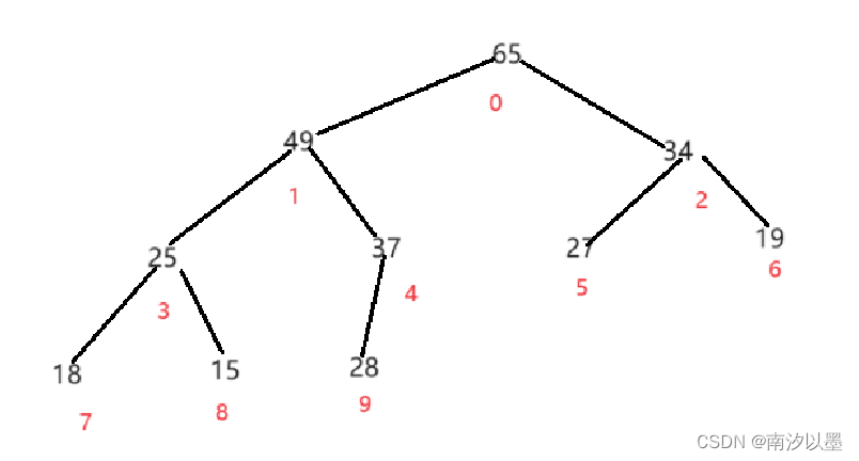
假设我们添加90这一个元素且以37——28树为例,那么这下子我们这个二叉树也要进行调整了。
因为假设我们90是大于37的,所以我们要调整为大根堆,要把90和37交换位置,进行向上调整。
但是,我们调完一颗子树就行了吗?肯定不行的,当我们把90放到28的位置后,发现,90的父节点又小于90了,所以以90的父亲节点一直进行向上调整,直到堆顶。
public void offer(int val){
if(isFull()) {
arr = Arrays.copyOf(arr, 2 * arr.length);
}
arr[UsedSize]=val;
UsedSize++;
shiftUp(UsedSize-1);
}
public boolean isFull(){
return arr.length==UsedSize;
}
public void shiftUp(int child){
int parent=(child-1)/2;
while (parent>=0){
if(arr[child]>arr[parent]){
swap(child,parent);
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}
当然,插入之前肯定要判满,满了就扩容。
这次插入呢,我们先确定了child位置,知道child也容易知道了parent位置。
有插入就有删除咯,那我们接着介绍另一个方法:poll
poll:
这个删除操作,先说明不是真正意义上的删除,因为你已经往数据插入数据了,即使改为0也不行,万一数据就是0呢?
所以我们删除逻辑是这样的:
以这幅图为例:
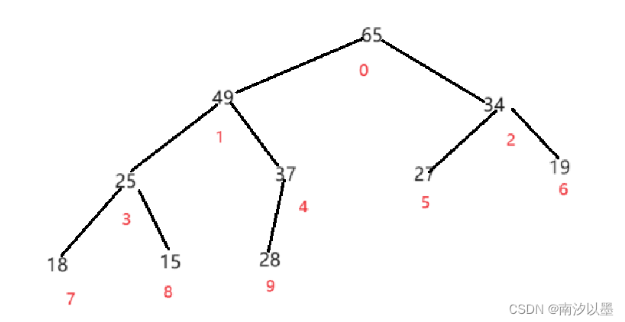
将我们的28和65交换位置,然后让UsedSize--,到了下标为8的位置,接着,让0(28)下标和UsedSized分别作为开始和结束进行向下调整,直至成为大根堆:
public int poll(){
if(isEmpty()){
return -1;
}
int old=arr[0];
swap(0,UsedSize-1);
UsedSize--;
shiftDown(0,UsedSize);
return old;
}
public boolean isEmpty(){
return UsedSize==0;
}
同样的,删除,也要进行判空。为空,给个-1呢,也可以进行其他操作。
ok,讲到这里我们的堆就讲完了。
完!
